Spiral Galaxies
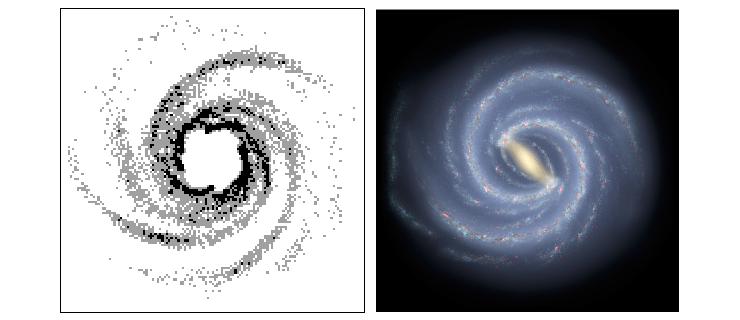
Left: Spiral structures that form in our model spontanously. Right: An Artist's impression of the Milky Way. Credit: NASA/JPL-Caltech/ESO/R. Hurt. Both pictures cover 40 x 40kpc.
Spiral galaxies ask us many a riddle. I give new answers to some of them by constructing self-consistent models for spiral galaxies whos dynamics are close to observations. These models allow a new view on the dynamical evolution of these galaxies. For the present I restricted myself to a model for the Milky Way.
On this page I give a short overview over the major results of my work and show some videos of simulations which (naturally) cannot be shown in the printed paper. The paper can be found on arXiv: arXiV:2203.08672.
The model
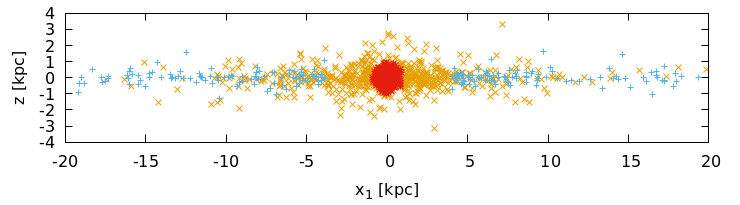
A cross section through our model. The Interstellar Medium (ISM) (blue +) is the dynamical part of our model. We ristrict it to a razor-thin disk and use a Plummer potential to pay attention to its disk thickness.
In our model the Interstellar Medium (ISM) is equipped with self-consistent dynamics where all mass is moving on almost circular orbits. Bulge (red *) and stellar disk (orange x) are implemented as rigid components. We try to reproduce with our model both the circular velocity curve of the Milky Way, as measured by Eiler et al (2019), and the observed dynamics of the ISM.
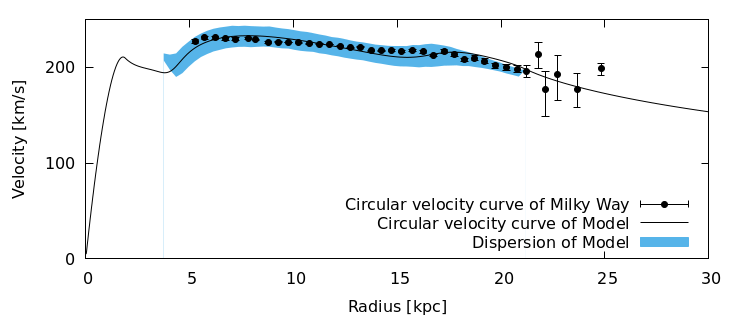
Our model fits the circular velocity curve of the real Galaxy very well. The velocities in the ISM are close to the circular velocity. The dispersion of velocities, i.e., the thickness of the blue stripe, can be chosen freely.
A minimal Mass Gap
The model does not use Dark Matter (DM) and - comparing it with current models - we see that the missing mass distributes uniformly over the baryonic components. Each component has to be about three to four times more massive than currently assumed. The total mass within a ball of 21kpc matches the total mass (including DM) of current galaxy models. So the mass gap between our model and observations is as small as possible. We could have included a DM-halo in our dynamical model, but the instabilities, which we discuss below, take care that our DM-free model behaves like the real galaxy. Therefore we want to discribe this very interesting, purely barionic model here.
Self-excited Spiral Structures as the result of an instability
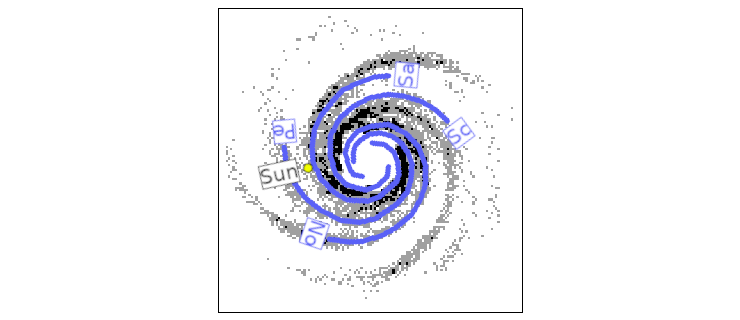
Black/gray: Spiral arms that form in our model spontanously. Blue: Observed spiral arms in the Milky Ways ISM.
The picture shows how after 400My the initially axially symmetric disk of the ISM (blue + in the cross section above) has developed four clearly defined spiral arms. We have overlaid this picture with the spiral arms found by Cameron-Steiman et al (2010). Given that the spiral arms in our model develope spontanously out of an initially axially symmetric disk, the similiarity is surprising.
In the plots black corresponds to densities above 120 M☉/pc2, gray to densities above 60 M☉/pc2 and white to densities below. The pictures covers 40 x 40 kpc.
In the following video you can study the evolution of the model in more detail:
We need your consent to load content.
In order to show videos we use the services of third-party providers. These providers can collect data about your activities. Further details can be found under “Learn more”.The simulation shows one out of ten particles that were used for running the simulation. The diagram in the top right shows the tangential component of the velocity plotted against distance from the galactic center for a random sample of one hundert particles. The purple dots in this diagram mark the 'local circular velocity' at a particles position, i.e., vc,loc = √(x⋅∇U(x)). In axial symmetry these dots form a straight line and respresent the circular velocity curve; while the spiral activity is strong, they are scattered. The middle right diagram shows the density averaged over an annulus around the galactic center. The bottom panel shows the RMS of the tangential accelerations as a function of time. While the disk transforms from axisymmetry to a state with spiral arms, this RMS grows exponentially.
It should be noted that the spiral structure in this model is self-excited. There are no external disturbations. The structure forms directly out of the shot noise that is due to drawing the initial particles at random from the model.
In this simulation the initial low dispersion of velocities grows due to the spiral activity; top right diagram in the video. This higher dispersion stabilizes the disk and the spiral activity vanishs. In the real galaxy the disipative process of cloud-cloud collisions in the ISM takes care, that the dispersion does not rise. Thus in the real galaxy the spiral activity can last (almost) forever. We have not modeled this disipative process yet.
The observed Dispersion of Velocities and the Jeans instability
This disipative process must be strong since it keeps the dispersion everywhere in the galaxy at the same low value somewhere around 10 km/s. But although it is strong, it does not decrease the dispersion to zero. Why?
In our models the Jeans instability can give an answer to this question. In the following video you can observe this instability in action.
We need your consent to load content.
In order to show videos we use the services of third-party providers. These providers can collect data about your activities. Further details can be found under “Learn more”.The video shows three simulations which have all a very similiar, DM-free mass model but different dispersions. The left simulation shows a cold disk; all mass of the ISM is initially on circular orbits, the dispersion is zero. The middle and the right simulations show cool disks; in the middle one a dispersion of 9km/s and in the right one a dispersion of 11km/s was chosen. Both of the left simulations are unstable while the right one is stable. The instability, that destroys the two left disks, is called the Jeans instability. It triggers only if the dispersion of velocities is too low.
To suppress the formation of spiral structures in these simulations, axial symmetry was enforced.
The Jeans instability does not only rearrange the masses but also increases the dispersion of velocity. Therefore a disipative process - however strong it may be - cannot reduce the dispersion below the threshold between stability and the Jeans instability. Because if it does so, the Jeans instability starts to work against it. This stability threshold lies in our models around 10km/s and coincides with the observed dispersion in the Milky Way's ISM.
